現職中研院數學所助研究員。以前在美國東西岸念過和教過書，覺得回來臺北比較快樂。照片是在法國研討會的週末拍的，表情顯示覺得數學很難。

▲作者於 2022 年暑假參加法國高等科學研究所 Langlands 綱領研討會之海報截圖。

在複雜的現代社會裡，我們會在各種小地方與數字有關的小問題不期而遇。比如說，我想要為一款遊戲設計一個方格狀的棋盤，裡面有五種顏色的方格：

上圖的設計有一些對稱性，像是：
1. 讓盤面無限延伸的話，每種顏色出現的頻率和方式都一樣。
2. 把同色的方格連起來，也會形成一個正方格狀的結構。
讀者可以發現，大的正方格面積是小方格的五倍。這是因為我們有畢氏定理：2²+1²=5
如果小方格的邊長與面積是 1，那麼大方格的邊長是 √5，面積是 5。這也說明了每種顏色佔據的比例是五分之一，所以五種顏色正好填滿棋盤。這給了我們一個有趣的小觀察：

「同樣的設計，對三種顏色或是六種顏色行不通，因為 3 和 6 不能寫成兩個整數的平方和。」

這就給了我們一個信手拈來的關於數字的小問題：有哪些數字（整數）可以寫成另外兩個整數的平方之和呢？比如說 4=2²+0²、8=2²+2²、9=3²+0²、10=3²+1²、13=3²+2²。中間被我們跳過的 3, 6, 7, 11, 12 則不能寫成兩個整數的平方和。法國數學家吉哈（Girard）和費馬（Fermat）都曾提出過以下的觀察：

定理 A：一個正整數 n 可以寫成兩個整數的平方和的條件如下：n 可以寫成一個平方數和一些質數的乘積，使得這些質數都可以寫成兩個整數的平方和。

比如說，45=3²×5，而我們也可以從 5=2²+1² 推導出 45=6²+3²。反過來說 12=2²×3，而 3 不能寫成兩個整數的平方和，12 也不行。又比如 15=3×5， 其中 3 不能寫成兩個整數的平方和，於是 15 也不行（儘管 5 可以）。一般來說，哪些質數可以寫成兩個整數的平方和呢？我們有：

定理 B：一個質數 p 可以寫成兩個整數的平方和的條件是：p 除以 4 的餘數不等於 3。

好比像 2=1²+1²、5=2²+1²、13=3²+2²、17=4²+1²、29=5²+2² 這些除以 4 的餘數都不是 3。至於 3, 7, 11, 19, 23 這些除以 4 餘 3 的質數，就只能乾瞪眼了。

在我們看更多例子之前，讓我們談談上面這兩個定理的原理。首先，讓我們提煉一個在本文會一直若隱若現的哲學：

「關於整數的問題，經常可以分解成關於每個可能的質（因）數的問題」

有興趣閱讀完整定理 A, B 證明的讀者可以參考維基百科關於「費馬平方和定理」的條目（英文條目「Fermat’s theorem on sums of two squares」有比較多的內容）。通常在大學代數如果講到這個定理的話，會從如下的引理出發（詳見英文條目裡 Dedekind 的第二個證明）：

引理 C：對於一個質數 p，存在整數 n 使得 n²+1 是 p 的倍數的條件等同於定理 B 的條件，也就是 p 除以 4 的餘數不等於 3。

前面定理 A、 B 和引理 C 都是數學家所研究的對稱性：

「用一種方式表述的結構（好比一個☆符號、或是能寫成兩平方和的質數），在另一種操作底下（旋轉 72 度、或是除以 4 取餘數）保持不變。」

在數論（研究整數的數學）中，有一系列像前述這樣子，相當奇特的對稱性。讓我們看看更多例子。比如說，引理 C 的高次方變體是：

定理 D：對於任意兩個相異質數 p 和 q。以下兩個條件等價：
Ⅰ. 存在整數n使得n^p-2+n^p-3+…+1 是 q 的倍數。
Ⅱ. q 除以 p 的餘數是 1。

接下來這個例子更神奇了。考慮無窮級數

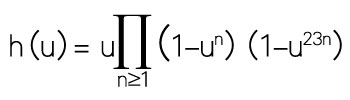
=u（1–u）（1–u²）…（1–u²²）（1–u²³）²（1–u²⁴）…（1–u⁴⁵）（1–u⁴⁶）²…
=u–u²–u³+u⁶+u⁸–u¹³–u¹⁶+u²³–u²⁴+u²⁵+u²⁶+u²⁷–u²⁹–u³¹+u³⁹–u⁴¹–u⁴⁶–u⁴⁷+u⁴⁸+u⁴⁹–u⁵⁰–u⁵⁴+u⁵⁸+2u⁵⁹+…
（喜歡計算的讀者，可以享受一下把上一行乘起來得到下一行的過程）

定理 E：對於質數 p，以下兩個條件等價；
Ⅰ. 存在整數 n 使得 n³－n－1 是 p 的倍數。
Ⅱ. 在無窮級數 h（u）裡，u^p 的係數非負。（這時它們的係數一定是 -1）

比如說，在上面的級數中，對於 p=2, 3, 13, 29 等質數，up 的係數是 -1。其他係數不是 -1 的質數（最常見的是 0，第一個正係數的質數次方是 u²³，再來是 2u⁵⁹）像是 p=5, 7, 11 等，就存在整數 n 使得 n³－n－1 是 p 的倍數，比如 2³－2－1=5 是 5 的倍數，5³－5－1=119 是 7 的倍數等等。

讓我們再瞪著上面的級數看幾眼，它有幾個令人想吐槽的問題。好比說，為什麼要有 u 的 23 次方呢？23 這個神奇數字 x³－x－1 這個三次多項式的判別式，但更令人抓狂的是……好吧！就算有 23 好了，那為什麼是上面這個神祕的無窮級數呢？

再看一次這個無窮級數：

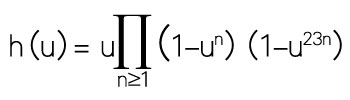
=u–u²–u³+u⁶+u⁸–u¹³–u¹⁶+u²³–u²⁴+u²⁵+u²⁶+u²⁷–u²⁹…
它有一系列美妙的性質，比如：
Ⅰ. 每當 a, b 是兩個互質的正整數，在無窮級數 h（u）裡我們都會有 u^ab 的係數 = u^a 的係數 × u^b 的係數。
例如：
． u² 和 u³ 的係數都是 -1，而 u⁶ 的係數果然是 -1 × -1= 1。
． u⁴ 的係數是 0，對所有奇數 k， u^4k 的係數（例如 u¹², u²⁰, u²⁸）都是 0。
． u³ 的係數是 -1，u⁸ 的係數是 1，而 u²⁴ 的係數果然是 -1 × 1= -1。
順帶一提，我們的無窮級數若是沒有乘上（1–u²³ⁿ）的項，那麼 u²⁴ 的係數就會不一樣，這個特別的性質也就不會成立了。

Ⅱ. 上面那些係數是 -1 的質數（p=2, 3, 13, 29）等等都可以寫成 2x²+xy+3y² 的樣子，其中 x, y 是整數。
例如：13 = 2 × 2²+ 2 × -1+ 3 ×（-1）²。這裡 2x²+xy+3y² 的判別式也是 1²– 4 × 2 × 3 = -23（我們的 23 又出現啦！）。總之，這個無窮級數還有幾個這樣特性。

其中最厲害也最神祕的特性，需要考慮將 u 帶入複數的值。讓我們對無窮級數 h（u）帶入 u = e^2πiz，其中 z 是任何虛部大於 0 的複數。讓我們寫做 f（z）=h（e^2πiz）。由於複數指數函數 e^2πiz 的性質，我們有：
a. 在 z 的虛部大於 0 時，|u|<1，從此可以證明無窮級數收斂。
b. 由於 e^{2πi（z+1）} = e^2πiz，我們有 f（z+1）=f（z）。
不只如此，我們還有：

定理 F：函數 f（z）=h（e^2πiz）滿足方程式：

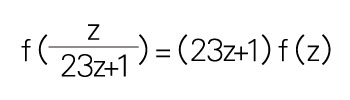
定理 F 完整的描述是：

定理 G：對於任意整數 a, b, c, d 滿足 ad – bc = 1，且 23 整除 c 和 d–1，我們有：

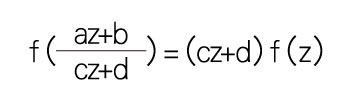
（定理 F 是定理 G 在 a=d=1, b=0, c=23 時的特例。）

滿足定理 G 的函數稱為一個模形式（modular form）。模形式有高度的對稱性。把關於變數 z 的對稱性畫出來，大概像這樣：

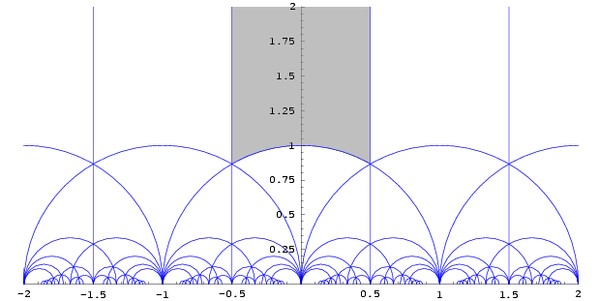
▲僅為示意圖；上圖是沒有考慮 23 的情況。作者表示：「23 這個數字有點大，我不會畫。」

現在我們可以跟大家分享標題裡的 Langlands 綱領是什麼。這是數論近來來最重要的領域之一。你可以說 Langlands 綱領是一套哲學，它表述的是：

「每個多項式整數方程式，都對應到某個定理 G 這樣有極大對稱性的函數。」

上面這句話有很多模糊之處，比如「對應」到底是誰對應誰，以及怎樣算是「有極大對稱性的函數」；這些都有具體的陳述，但筆者沒有能力在幾千字的篇幅解釋。在比較簡單的情況，好比定理 B 和定理 D，我們的「函數」非常直接：除以 4 取餘數，或是除以 p 取餘數；定理 E 的函數 f（z）=h（e^2πiz） 則相當複雜。另一方面，「多項式整數方程式」的解的概念可以做相當的推廣。這需要用到抽象代數裡面「域擴張」（field extension）和「伽羅瓦群」（Galois group）的概念。

在 Langlands 綱領的研究裡，數十年來許多數學家累積起來的結果讓上面的句子不只是哲學，而是像本文的各個定理，是具體可以驗證的結果。好比說，讀者可能聽說過費馬最後定理：

「對於正整數 n ≥ 3，方程式 aⁿ+bⁿ=cⁿ 不存在正整數解。」

這個在 1995 年由 Wiles 以及他的合作者 Taylor 完成證明的定理，其證明正仰賴 Langlands 綱領的一個特別的情形。雖然這個證明有數百頁艱難的過程，我們可以用 Langlands 綱領的哲學來做個簡單的總結：
1. 首先將費馬最後定理化約到 n=p ≥ 3 是個質數，並且 a, b, c 互質的情形。
2. 假設方程式有正整數解，則我們可以考慮另一個方程式（Frey curve）： y²=x（x–a^p）（x+b^P）
這個方程式的性質是等號右邊的三個一次項 x, x – a^p 和 x + b^p 之間兩兩的差是 a^p, b^p 和 c^p，是三個互質而且各自有高度重複質因數的數字。接下來是真正困難的部分：
3. Wiles 和 Taylor 證明了此時的 Langlands 綱領：上述方程式對應到一個類似定理 G 的模形式。
4. 由 Ribet 在 1986 年證明的一個重要結果，我們可以把這個模形式化約到另一類更簡單的模形式。後者這類簡單的模形式只有有限多個，可以被一一列舉，從而檢查沒有一個可以是步驟 3 的模形式化約的結果。因此不可能有 y²=x（x–a^p）（x+b^P） 這樣的方程式。

最後，讓我們給幾句結語：現代的數學非常困難，往往在小地方就充滿了幾個禮拜也難以解釋的現象與細節。但數學的美妙之處之一是數學研究往往蘊含有富有解釋性的哲學（例如：Langlands 綱領），這些哲學可以用很精確的方式，來解釋一些具體的問題（例如費馬最後定理、或者設計遊戲的棋盤）。而我們數學家的工作，正是去找到這樣的哲學／理論、並且給出具體的解釋／定理。