後量子密碼學–以古典電腦抵禦量子破密

每種加密系統的根基，都是一道複雜的數學難題，而現在主流的公鑰加解密系統，包括 RSA 加密演算法、橢圓曲線密碼系統 (ECC)，背後的數學難題（大整數的分解因數問題，橢圓曲線上的離散對數問題）複雜得讓古典電腦一籌莫展，卻正好是量子電腦最擅長解決的問題型態。因為這些數學難題的答案，皆可轉化成週期性的結構，理論上，只要找到結構的週期，就可以「較為輕鬆」的破解問題。對於古典電腦來說，當數字相當巨大時，尋找週期仍是十分困難的任務，對於量子電腦卻是小事一樁。在 1994 年 Peter Shor 發明的演算法正好可以尋找週期，也就是能破解目前主流的所有量子密碼系統。相較於常見的對稱式密碼系統如 AES 只需要兩倍長的金鑰就可保證同樣的安全性，基於 RSA和ECC的公鑰密碼系統在夠大的量子電腦出現後便不再安全。因此，量子電腦蓬勃的發展勢必會威脅到生活中的隱私。

後量子密碼學（post-quantum cryptography，PQC）就是一個研究能夠抵禦量子破密的密碼學分支。在 PQC 中的公鑰密碼系統，主要歸類為以下五類：晶格密碼系統、編碼密碼系統、雜湊函數密碼系統、多變量密碼系統和超奇異橢圓曲線同源密碼系統。

後量子密碼學標準化競賽

為了迎接後量子密碼學時代的來臨，美國國家標準暨技術研究院（National Institute of Standards and Technology，NIST）自2016年起舉辦「後量子密碼學標準化競賽」，徵求新時代的加解密系統與數位簽章系統。在這場競賽取得最終優勝者，將成為新一代的標準化密碼系統。NIST 曾經舉辦過兩場競賽：千禧年前後的先進加密標準 AES 競賽和 2010 年前後的雜湊函數 (SHA-3) 競賽。成為最後獲選的 AES 和 SHA-3 的贏家的密碼系統的投稿人名利雙收。也因此，這次的競賽吸引了來自全世界的團隊參賽一較高下。2016年，NIST 在當年4月於日本福岡舉辦的 PQCrypto (後量子密碼學) 會議上宣布開始徵集後量子密碼系統參加競賽。而 2017年11月30日截止收件時共有82組投稿。經過一番簡單的檢查，同年12月21日(聖誕假期前夕的週五)公告上網有 69 件合格的稿件。

比賽的故事

民間故事中煉蠱的過程是把毒蟲全部丟進一個水缸，活著爬出來的就是蠱王。其實這個競賽好像也沒有什麼差別。NIST 的人員公告了誰進入第一輪就回家放假過節了。但是密碼學家多數都是阿宅 (不分男女老少都是)。眾所週知，阿宅是不過節的。美國當地時間12月21日的晚上就有密碼學家破了其他人投的系統。四個月之後的第一次後量子標準化會議在佛羅里達召開時，已經有 ¼ 投稿的密碼系統被徹底擊破或是嚴重受損。

次年 (2019) 的一月31日，因為川普關閉聯邦政府而跟著關門關了快一個月的 NIST 重新開門辦公不久就公告了 26 組晉級第二輪的密碼系統。當年八月，NIST 在加州 Santa Barbara 大學舉辦第二次後量子準化會議。翌年 (2020) 的7月23日，NIST 公告了晉級第三輪的密碼系統。 經過兩輪的篩選，這時已經剩下15組人馬，被分為七組決選者 (finalist) 和八組備選者 (alternate)。決選者中，有五個晶格密碼系統、一個編碼密碼系統和一個多變量密碼系統。備選者中還有兩個晶格密碼系統。晶格密碼系統顯然因為其總體性能優越而佔了絕大多數的晉級名額。

中研院本有相當強的密碼學團隊，這次比賽也沒有缺席。通過了第一、二輪的考驗，我們參與了兩組決選者 (數位簽章系統Rainbow，和加解密系統 Classic McEliece) 和兩組備選者 (數位簽章系統SPHINCS+，和加解密系統NTRU PRIME)。距離成為世界標準，似乎只剩一步之遙。在這過程當中，筆者的 Rainbow 團隊還成功的破解了和 Rainbow 最接近的競爭者，同屬多變量數位簽章系統的 LUOV。

爭議

在 Rainbow 入選第三輪，和跟它同類的系統 GeMSS 也受到致命的攻擊之後，它本來被看好成為標準。但是 LUOV 的發明人之一，一位年輕比利時人 Ward Beullens，站出來復仇了。Beullens 發現了 Rainbow 結構上的一個問題，並主張因此 Rainbow 的安全性不足。筆者代表團隊進行了一系列的分析並得到結論：我們的系統在 Beullens 攻擊下還是有足夠的安全性。然後雙方和 NIST 就到底誰的分析比較精確爭議了數個月之久。但是聰明的 Beullens 此時發出了更凌厲的一擊。基於相同的結構問題他發現了另一個攻擊，並破解了 Rainbow 最小的參數。這個攻擊或許並不是根本性的，或許 Rainbow 可以換個大點的參數仍然安全，但是它已不可能選上了。

與此同時晶格密碼系統也出現學理和法務上的爭議。學理上有人 (D.J. Bernstein) 主張某種攻擊是可以破解 Kyber 和 SABER。但另一派密碼學家對 Bernstein 的結果極力否認。

法務上的爭議是這樣的: 決選者中的 Kyber 和 SABER 都有可能的專利覆蓋，有¼ 個世紀歷史的老牌 NTRU 系統則是沒有這個問題。有專利覆蓋的系統如果成為標準，就相當於在為特定人牟利了。剛剛提到的那一派人則極力主張專利上沒有問題。

持有專利者在法院獲得了一些勝利之後。Kyber 和 SABER 的命運看來似乎也就決定了。
但最後 NIST 決定花錢買下這兩個專利，並選擇 Kyber 為最後的勝利者。由於之前吹哨者 Snowden 事件中已經有人指控過美國國家安全局 (NSA) 能夠指揮 NIST，因此 NIST 究竟有何想法受到一些質疑。

其他的選拔結果

除了 Kyber，加解密的晶格密碼系統均被宣判出局，NIST 宣告兩個晶格體系的數位簽章系統 Dilithium 和 Falcon 都是新的標準 (Dilithium 是屬於和 Kyber 的同一派系支持的，但在很多性能考量上 Falcon 要更好)。另外基於雜湊函數的簽章 SPHINCS+ 也因為它廣被接受的安全性而被選為標準。資訊所的倪儒本老師是 SPHINCS+ 的共同提出者，我們也要恭喜他。

同時NIST另外開了一個給數位簽章的選拔，咸認他們心目中的目標是上個世紀發展出來的多變量系統 UOV。中研院團隊也將參與這個系統的投稿。他們也宣告幾個加解密系統 Classic McEliece, BIKE, HQC, 和 SIKE 繼續進行第四輪選拔。

實作和組合語言的重要性

雖然競賽暫時落幕，但是為了這個競賽所做的研究並不會消失。中研院在晶格密碼系統的計算上投注了大量的心血，主要在晶格密碼系統 Dilithium、Kyber、NTRU、NTRU Prime和SABER。我們並專注於這些密碼系統中最消耗時間的計算：多項式乘法和其變換。

C語言是一個通用程式語言。因其精細的記憶體調控能力，資深程式設計師所寫的C程式通常被視為優化的實作。然而在密碼學實作上，C程式通常只被做為參考實作，而不論及效能和各平台的安全性。密碼學實作中，目標是寫出全世界最快的程式，記憶體配置只是其中一個影響因素。效能良好且安全的實作常常用到平台的特殊指令和組合語言。

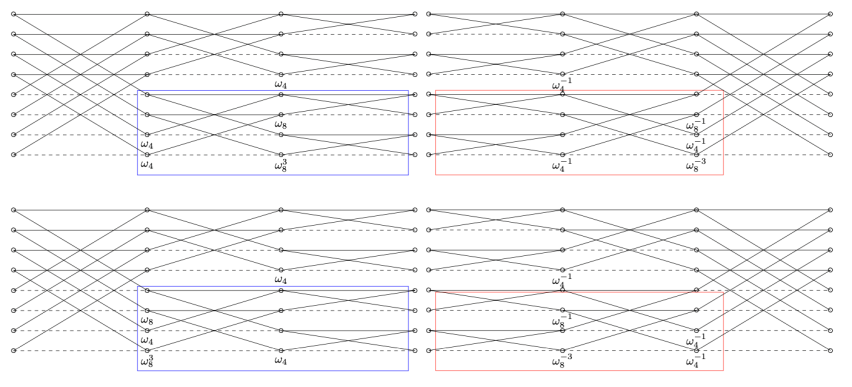
在這幾年間，中研院開發出很多的手法來實作晶格密碼學，特別是在快速傅立葉變換 (Fast Fourier Transform, FFT) 和數論轉換 (Number Theoretic Transform 或 NTT, FFT 用在整數環的一種特化) 的實作技巧上堪稱獨步全球。上圖是其中之一，我們開發出來新版的蝴蝶變換 (butterfly) 用來加速晶格密碼學中最重要的 NTT。中研院也是最早提供形式驗證作用於快速晶格密碼學組合語言程式並證明為正確的出處。

將來與願景

不論最後結果這個世界是採用哪個或哪些系統，中研院的密碼學團隊希望提供給全世界快速、安全、正確、廣用的程式庫，同時也對後量子密碼系統的安全性做出更精確的評量。還請大家拭目以待。