顆粒體的流動(Granular flows)到處可見,例如古埃及人建造金字塔、漢人蓋長城,涉及了建築工地處理砂石;還有廚房裡洗米選豆子、餐桌上加糖加鹽、精密製藥如何均勻攪拌,甚至火星探測器著陸後要怎麼行進,都有顆粒體的流動。
然而,關於顆粒體的研究,可以說一直處於三不管地帶,並不像流體力學、固態結構力學在西方科學各有上百年的傳統。物理學家積極參與顆粒體研究大概也是近幾十年,尤其在「非線性力學」的熱潮之後才開始。這種困境當然有它的歷史因素,且光是觀念上的出發點以及使用的語彙,就足以陷入無止境的爭論(圖1a)。
但是對局外人而言,一門仍然在草創階段的學問,卻是個一窺科學家如何試圖化繁為簡,在困境中尋找出路的大好機會。舉例而言,顆粒體流動的方式有很多,我們不妨將沙漏(hourglass)上半部常見的「緩慢」流動現象,對照讓人聞之色變、「快速」流動的流沙(quicksand),就可輕易提出第一個問題:我們憑什麼來定義「快/慢」?
除此之外,還有一種特別的流動:間歇流(intermittent flows),瞬間爆發的能量往往造成極大的災難──在土石流及地震時有所聞的臺灣,更是不可忽略的議題。但是科學家們對這些顆粒體的瞭解,相較於傳統的流體或固體,若說仍然束手無策並不為過(圖1b)。
何謂「流動」?「主角」是誰?──純粹思考vs.現實世界
話雖如此,有一些自古以來的「套路」還是可以用的。在此我們介紹兩個概念,應足夠大家貫通以下要談的小故事。
首先,是關乎怎麼「描述」流動。舉個最簡單的例子,如圖2a所示,假如要從上面驅動下方的一大堆物質──可以是一大塊能夠變形的橡膠、或是一堆沙子,甚至只是純粹的流體(例如:水),會產生位移,並且不同深度位移不一樣。
因此談到「流動」,我們關心的是位移(Δx)隨著深度(z)的「差異」。這個差異,內行話叫做位移的梯度(gradient),可以視為形變的程度──更精確的說,若排除「轉動」成分,這個梯度描述了所謂切應變(shear strain)。很多情形下,我們更關心這個應變隨時間的變化率,也就是「速度」的梯度,簡稱為切變率(shear rate),單位是時間的倒數。
換句話說,切變率告訴我們「要花多少時間(的倒數)」來看到這些物質「已有相當程度的流動」: 正如圖2a原先垂直排列的圓球「流動」到大約45度傾斜(shear strain~1)。切變率的大/小,形容的已然是一種快/慢的趨勢──但這樣只能叫做「趨勢」的描述,還談不上已界定出快或慢的本質「意義」是什麼……
若要討論「意義」,就要先能把互相影響、甚至競爭的各種因子整理出可用的「評分指標」,這觀念叫做建立「無因次量(dimensionless parameter)」,這些指標不帶物理單位,是絕對的數字──但有趣的是,物理學家的首要工作幾乎可以說就是在定義這些不帶物理單位的數字!
「無因次量」聽來神奇,其實並不罕見。大家也許常常聽到用雷諾數(Reynolds number)來描寫流體紊亂(turbulent)/平穩(laminar)的程度,而這正是物理學家分析過慣性力(inertia)與黏滯力(viscosity)的相對比例後所歸納出來,告訴我們什麼情況之下流體力學該以哪些作用為首要考量──畢竟如果把所有可能的作用都一視同仁地算進去,很可能連近似的樣貌都猜不出來,更遑論「完整」解答!
另一個,軍事迷必定聽過的例子,叫做馬赫數(Mach number)──具體的定義是移動物件的速度相對於聲波行進速度的比值,而其隱藏的意義則是在這種運動狀態下流體可能被壓縮的程度──這數值如果很小,前輩們給我們的保證是把這些流體當作「不可壓縮」的介質來處理就綽綽有餘了。
然而,流體力學經過了兩百餘年的耕耘,這些指標已經多到不勝枚舉。反觀顆粒體的流動,我們又知道多少呢?
在學術界,過去二十年來對顆粒流歸納出的無因次量,較為人接受的不外乎以下兩者:Inertia number通常被用來描述乾顆粒的物理 [1],考慮顆粒之間「完全沒有」液體的情況;相反的,Viscous number(J)則是用在固體顆粒完全浸在液體裡面,且這些液體對整體的流動以及作用力有相當程度的影響(甚至成為主角)[2]。
然而,現實往往介於兩者之間,不是非黑即白。更常見的情況是一大堆顆粒緊緊地被壓在有液體的環境裡頭:這些液體雖然可以影響固態顆粒表面而有「潤滑」的效果,但是就「力的傳遞」來看,主角還是顆粒與顆粒之間的直接接觸,更精確地說是其錯綜複雜的「網路」,且不難想像緊密度一旦下降到一定的程度,這些液體又可能變回主角──這不正是自然界很常見的狀態嗎?

圖1.顆粒流(granular flows)研究的困境及現象的多樣性
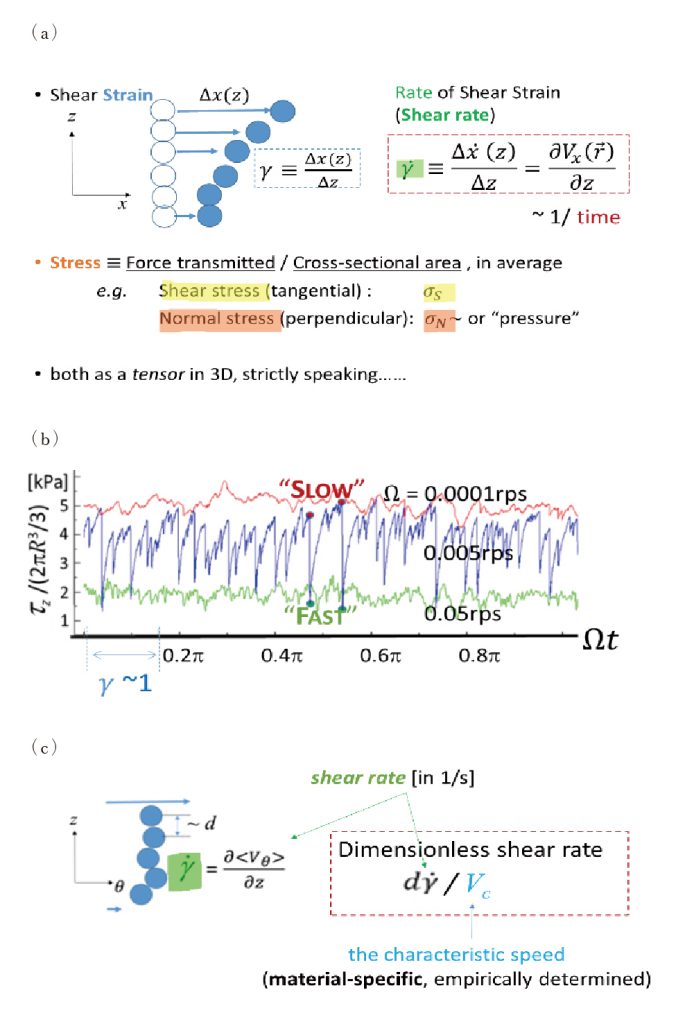
圖2.(a)何謂「流動」;(b)本團隊的實測例;(c)無因次量slipperiness。
「奇怪」的發現,也可能是撿到遺落的貝殼……
過去幾年,我們在物理所的小團隊發展的實驗就是基於這樣的概念[3]:我們使用自己合成的公分大小「軟」顆粒圓球──其彈性只比文具用的橡皮擦略硬,將它們緊緊地壓在特製的兩個錐形之間。在保持「總體積不變」的條件之下,我們藉由轉動來施以恆定的切變率。同時顆粒之間填有液體:液體在顆粒被緊壓的情況下,不會是「力」的主角,但在適當的調配下,可讓其對光的折射率和這些固體圓球一致。換言之可見光在經過顆粒之間的時候就不再有折射的現象,讓我們可以只用肉眼或光學攝影機就「看見」內部的顆粒在各種轉速下的動態──典型的例子可參見網站所附影片 [4]。
採用這種「軟」顆粒的用意是即使在「緊壓」的狀態下,仍讓我們可有足夠的動力及機械強度來維持快慢相差可達數百倍或更大的「定速轉動」。
圖2b顯示我們使用完全相同的液體及顆粒密度,所測量出要維持三個不同轉動速度時,系統所需承擔的轉矩的起伏:在「低」轉速下(Omega=0.0001rps),轉矩最高;在「高」轉速下(Omega=0.05rps),轉矩偏低。更值得注意的是,在「中等」轉速,轉矩呈現了不規則且形似於「地震」的劇烈起伏,拍攝到的光學影像也證實了在轉矩陡降的同時,系統內部發生大規模的集體崩動──這些該怎麼解釋呢?
後見之明是,我們在學基礎物理時將「摩擦係數」當作是與運動狀態無關的常數這個概念,雖已習以為常,卻和事實相差甚遠!話說回來,「摩擦係數並非常數」並不是新發現,但為了讓理論簡單的確是常被採用的簡化。這雖無可厚非,卻使得數十年來前輩們的理論模型都不知不覺地排除了以上觀察到的諸現象!
於是,透過其他獨立實驗,確認這些固體顆粒表面之間的「摩擦係數」在達到一定的速度(Vc,和材質及液體都有關)之上確實會呈現顯著下滑之後,我們提出了專屬於緊密顆粒流動所需的無因次量──姑且稱之為slipperiness(圖2c):即使我們難以預知所有顆粒之間相對的速度,但是顆粒的大小(d)及「速度梯度」(即前述shear rate)」兩者的乘積,至少給出了這些相對速度大致的「量級」。
這個「量級」和Vc組成的比值,就預告了系統裡顆粒之間摩擦係數因為相對速度超過Vc而減損的程度。其實,地質學家在數十年前也早已認定岩石間他們普遍稱之為“velocity weakening”的現象正是地質不穩定的必要因素,所以這仍然不算「新聞」……。
曙光乍現:前輩的肩膀&海平線的另一邊
故事進行到這裡,我們終於有機會將看似互不相容的「劇情」融入一個統整的框架裡。
參考圖3,在「夠緊密」的情況下,slipperiness這個新參數,連結了我們稱之為「固態(granular solid)」以及「液態(granular liquid)」兩種極端:兩者分別代表了「摩擦完全沒打折」(因此需要很高的轉矩才能夠推動),以及顆粒間摩擦力喪失殆盡以致「完全液化」的相反狀態──就如在流沙的掙扎恰使得砂粒之間在靜止時還可能存在的摩擦力完全失效[5]。
居於兩極端之間的,則是更「危險」的局面,也就是間歇流。顆粒間或許有相當比例的接觸是處於高摩擦的狀態而形成壅塞,且在系統被外力驅動的同時,顆粒間的接觸力以及能量持續累積上升──但驅動的轉速又不可能允許大多數的接觸永遠維持低於Vc的相對速度;一旦有相當比例的接觸,滑動速度超越Vc,使得該處的摩擦力開始下降,就很容易觸發更大規模的快速移位,直到新的壅塞組態再度形成。
然而這短暫的遽變,往往釋放驚人比例的能量。這相當於我們得以在實驗室裡用穩定的轉速持續製造「地震」來做統計研究──至少概念上如此。
除此之外,我們也釐清了為何前輩們使用Viscous number的典範在顆粒「足夠緊密」的情況下往往失效。因為在該「J-rheology」的思維之下,顆粒間被想像成一直包裹著某種厚度以上的液體,當然也斷不可能容納因「接觸」而讓摩擦生效,也談不上此摩擦是否隨相對速度有所改變。
然而,在我們提出的這個圖像裡,顆粒的這種懸浮態(granular suspension)可視為是「第三態」,但又和此圖右上方「完全液化」的狀態無縫相連,兩者可併稱為和固態相對的「流態(granular fluid)」,卻不像前述兩種極端情形之間會有「間歇流」這道涇渭分明的界線。
當然,這一切只是個開始。我們的初步成果解讀了「動靜之間」的局勢消長。但若要完整地理解這個圖像,還需要進一步釐清「鬆緊之辯」──這是否意味著另一個無因次量的出現,以及這思維能否讓我們為理解間歇流,乃至於真實的地震現象,貢獻棉薄之力,就請各位拭目以待吧!
[1]Forterre and Pouliquen, Annu. Rev. Fluid Mech. 40(1), 1–24. (2008)
[2]Guazzelli and Pouliquen, J. Fluid Mech. 852, P1 (2018).
[3]Jih-Chiang Tsai, Guan-Hau Huang, and Cheng-En Tsai, “Signature of Transition between Granular Solid and Fluid: Rate-Dependent Stick Slips in Steady Shearing”, Phys. Rev. Lett. 126,128001 (2021)
[4]https://www.phys.sinica.edu.tw/jctsai/brittle/
[5]有一種說法是:其實一旦流沙底部的地下水被攪拌到上層,只要能夠不驚慌,仰躺保持口鼻在沙水面之上,其實人體的總密度是略小於水的,因此並不會持續下沉。但能這樣自救的前提是身上沒有重物,更重要的是在驚慌之中沒有失足踩入深層的爛泥或者其他黏性更高的東西。然而後者一旦發生,若想抽離是非常困難的。換言之,在流沙裡發生的不幸事件,通常不真的是「沉下去」,而是被自己硬「拉下去」──詳見https://www.nature.com/articles/437635a
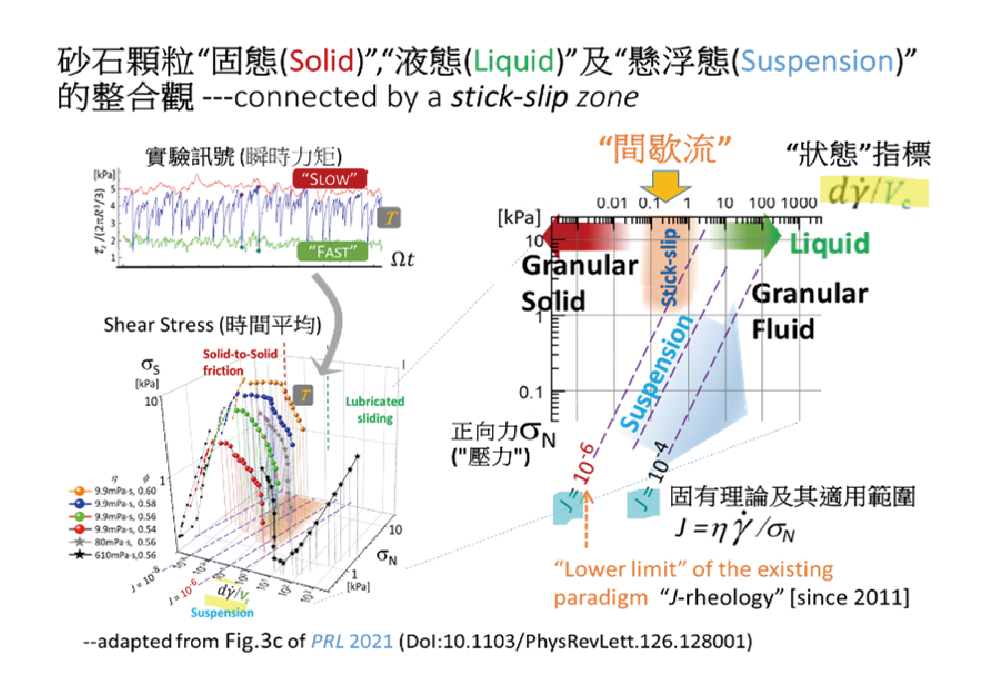
圖3.顆粒流「三態」的初步整合。
