你沒有看錯,要跟大家談論的題目就是「月光、怪物」。也許你會感到疑惑,名字會那麼奇怪,「月光、怪物」聽起來比較像手機遊戲或是科幻小說的名字。但我們不是要談論月光怪獸或是如何把你變成怪物。談論的是一個實實在在的數學問題。首先,我希望解釋一下這些怪名字的個中緣由,接著會說明它所引伸出的數學問題及理論。
什麼是怪物(Monster)和月光(Moonshine)? 根據英語字典的定義,所謂的怪物,是想像的、既大又醜又可怕。重點是它又大又可怕。不過如果你是30歲以下的年青人,對Monster的印象可能是PokéMon,他們是小巧可愛的。
那Moonshine是什麼?直接翻譯就是月光,是不太明亮、有點模糊不清。另一種比較靠近我們主題的解釋是不實在、空妄的,特別是指一些虛無飄渺的想法。另一種解釋是英國的俚語,Moonshine指的是走私或私釀的烈酒,一般是指威士忌。等一下大家就會明白為什麼要命名為Moonshine,因為它就像私釀酒一樣,沒有合法的地位。
實際上我們所說的Monster是一個有限群(finite group)。有限群的理論是從19世紀末期,伽羅瓦(Evariste Galois)有關多項式解的工作開始。他的工作後,群的概念就慢慢滲入數學的各領域,是現代數學中一個不可缺的工具。其中有限單群的分類更被喻為20世紀數學上的一個重大成就,現在我們知道任意一個非交換的有限單群G會同構於下列的一個群:
1.交替群Altn, n≥5;
2.一個Lie類型的有限單群(有16個無限家族);或
3.26個零星(sporadic)單群之一。
Monster(怪物群)是這26個零星單群中位數(order)最大的一個。英文中sporadic指的是零星、分散的,所以當這個群是sporadic時,就不能用一般的方法來說明它,不太清楚它從何以來,必須費心思去了解它。 Monster是sporadic群中最大的,但它有多大呢,會得到一個象徵恐怖的名字?Monster群的大小為
|M|= 2^46 3^20 5^9 7^6 11^2 13^3‧17‧19‧23‧29‧31‧41‧47‧59‧71 =808017424794512875886459904961710757005754368000000000
是一個54位數字。54位數聽起來似乎還好,但是如果認真算一下,它是非常可怕的,尤其當時的電腦還不是很發達。所以當發現有這個又大又可怕的對象時,就被命名為Monster。
那Moonshine又是什麼呢?沒辦法用三言兩語詳細的說明。它代表一個關於Monster群的指示標(character)和模函數(Modular Function)的神秘關係。模函數是數論中一類非常重要的函數,但它好像跟有限群沒有任何關係?當數學家們發現這樣一個奇怪關係時,當然想知道它是否正確?第二個問題自然而然就是為什麼是正確的。如果是正確的,那為什麼是正確的,有沒有一個好的解釋。重點是這類神秘關係把Monster的研究推廣到有限群之外,將Monster的研究帶到數論、李代數、甚至是物理的領域。
接下來讓我們討論一下什麼是有限群。有限群論是伽羅瓦有關多項式方程的工作開始。中學的時候,大家可能學過如何求二次方程式的解。二次方程〖ax〗^2+bx+c=0 可以利用開方根得到兩個解
x=(-b+√(b^2-4ac))/2a or x=(-b-√(b^2-4ac))/2a
重點是你只要利用開方這個程序及一般運算就可以得到方程式的解。那同樣的方法可以套用在更高次方的方程式嗎?如果是三次方、四次方的方程,是有類似的方法,解不是這樣簡單,但有個求解的演算法,只需要利用開方這個程序,就可以完成。大約在19世紀時,Abel給出例子,証明5次方以上的方程,不一定有開方解。伽羅瓦則是能使用開方處理與不可能的條件清楚寫出。他的想法是革命性的,把重點放在研究解本身的對稱性。何謂解的對稱性?一個方程通常有多個不同的解,有些解擁有相同的特性,有些卻不一樣。例如, x^2-2=0 這個方程有兩個解,一個是 √2,另一個是-√2。從代數的角度來看,兩個解是完全一樣,可以隨意調換。但 x^4-1=0 的4個解1,-1,√(-1),-√(-1)則需分成兩類,1,-1和 √(-1),-√(-1)本質上有所不同,解就無法隨意調換。伽羅瓦提出研究解的排列結構及置換的想法,他稱解的置換為一個「置換的群組」,這是群的由來。伽羅瓦從群的結構排列來確定方程有沒有開方解。現在群一般視為研究特定對象對稱性的工具。
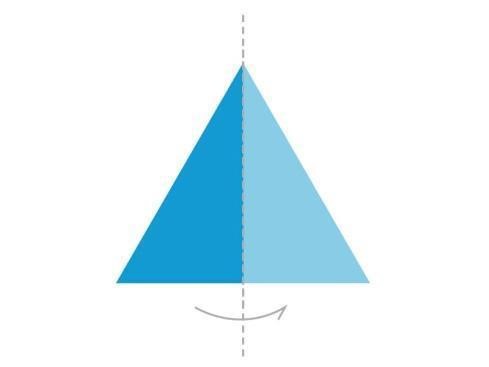
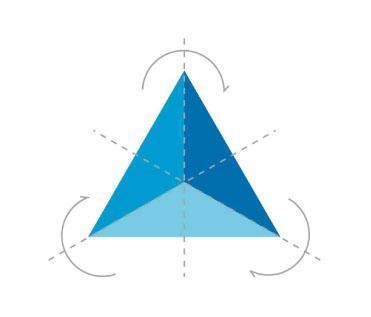
以全等三角形為例,利用反射使它左右交換,交換後,這個三角形是沒有任何改變,還是同樣的三角形。那如果同時做二次不同的反射,可以發現,三角形的頂點被旋轉了,三角形沒有改變。這樣一來,這個三角形的對稱性群有六個元素,三個是反射,另外三個是旋轉。我們也可以討論更高維的幾何物或一些複雜的代數系統。
接下來讓我們說明甚麼是指示標(character)。群是抽象的,所以希望用比較熟悉的工具來研究它,最常使用的工具是矩陣,因為可以做很多實質的計算。首先,我們知道在複數域C上,所有的n階可逆矩陣生成一個群,這個群稱為一般線性群及記成GL_n (C) 。一個從群G到GL_n (C)的群同態ρ:G→GL_n (C) 稱為群G的n維表現。一個特別的例子是把G全部對到單位矩陣,這是G的表現,稱為 trivial representation。有時候處理矩陣仍然困難,所以會考慮矩陣的跡(trace)。跡是指矩陣A對角線上各個元素的總和,一般記作tr A。當ρ:G→GL_n (C) 是G的表現,χ_ρ (g)=tr(ρ(g)) 被稱為指示標。跡是數字比較容易處理,但如果你只考慮複數域上的表現時,指示標本身就足以決定所有的不可約表現。當Monster群剛被發現時,數學家就嘗試計算它的指示標及不可約表現,其中一個發現是,如果Monster存在,它的最低維表現至少是196883維。
那Moonshine是怎麼被發現的? 故事源自以下一個非常簡單的等式:
1+196883=196884
這等式看來很簡單,小學生都可以理解,但它卻實是一個非常重要的發現。
之前提過1是trivial表現的維數,196883是Monster群最小不可約表現的維數。196884則跟橢圓j-函數(elliptic j-function) 的q展開有關。橢圓j-函數是一個重要的模函數,它是一個全純週期函數,所以可以把它展開成傅立葉級數。設q=e^2πiτ ,j 的q-展開式可寫成
j(q)=q^(-1)+744+196884q + higher order terms
John McKay 發現式子中的196884,好像和Monster有點關係,但又不太確定, 所以寫了一封信給John Thompson (當時最有名的群論學者),詢問他對這事的看法。經過很多的計算後,Thompson跟McKay 猜測怪物群存在一個無窮維的整數分級表現V=⊕_(n≥0) V_n,使得它的graded dimension
chV=∑_(n=0)^∞ dimV_n q^(n-1)=j(q)-744
他們還猜測,如果考慮分級跡(graded trace)
T_g (q)=∑_(n=0)^∞ trg|_(V_n ) q^(n-1),q=e^2πiz,g∈Monster,
這也是一個模函數。McKay-Thompson猜想強烈暗示怪物群(一個有限群)最自然的表現可能是無限維的, 這表示背後可能有更多我們不了解的結構存在。
這個猜想出現後,數學家們就開始計算這些級數的一些性質。Conway和Norton花了很久的時間去計算T_g (q)各級的係數,得到許多的數字但又不知道如何處理,就去圖書館,翻開一些有關模函數的書籍,在一本19世紀末的書中,看到許多數字跟他們算出來的一模一樣。他就猜測McKay-Thompson 級數應該就是書中所討論的函數。這之間充滿巧合,但是從這些巧合可以看到McKay-Thompson猜想並不是一個很輕率的東西,而是有實際證據,它背後應有非常漂亮的理論及很多我們不理解的事情需要我們去探索。Conway和Norton發現McKay-Thompson級數跟其中的171模函數相關,這些函數很特別,它們的modular curve都是genus zero,同時它們可以在模曲線上生成整個函數域。這發現非常有意思,為什麼Monster會跟曲線的genus有關?這個genus 0的特性到目前都沒有很好的解釋。
Modular Curves, Modular group 和相對的函數域在Monster 還沒出現之前,在數論中就被廣泛討論及研究。其中Ogg證明以下的定理:
定理(Ogg): 若 p 為質數, Γ_0^+ (p) 是一個 genus 0群若且惟若 p = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, 71。
如果仔細對比,你會發現這13個質數正好就是可整除Monster階數(order)的質數。Ogg有一次去聽演講時,聽到有關Monster的描述,其中整除Monster階數的質數和他定理中的質數剛好一模一樣,這樣的巧合當然引起大家的好奇。Ogg懸賞了一瓶Jack Daniels(威士忌的品牌)給任何一個可以說明兩者之間關係的人。
現在你可以比較理解Moonshine這個名稱的由來,Conway-Norton試圖去解釋怪物群和模函數的某種關係,也對Ogg的問題給出某些證據,但並沒有給出好的解釋,也沒有證明。他們可能應該獲得一瓶威士忌作為獎品,但所討論的關係及現象,嚴格來說沒有証明,在數學上仍末獲得“合法” 的地位,有點像「私釀的威士忌」,被稱為Moonshine也就一點都不奇怪。
1983年,Frenkel-Lepowsky-Meurman使用物理學上的頂點算子(vertex operator)構造出McKay-Thompson猜想中那個Monster群的表現,一般稱為Moonshine模。他們和Richard Borcherds引入了一個新的代數系統,稱為頂點算子代數(vertex operator algebra)。後來,又證明Moonshine模是頂點算子代數,並証明Monster群是這個代數的自同構群,那就是說Monster群是描述一個龐大代數系統的對稱性。這個模現在稱為月光頂點算子代數。
「頂點算子代數」的引入對「怪物群」的研究有非常深遠的影響。目前,我們可以透過研究頂點算子代數的結構和表現理論來了解怪物群,從前很多感到神秘的現象,現在都可以利用頂點算子代數來解釋。頂點算子代數也對物理上的保角場論(conformal field theory)提供了一個嚴格的公理系統和代數方法,而Monster是這種代數結構的對稱性。
「月光頂點算子代數」是一個龐大代數系統,研究它的對稱性非常困難,所以必須對它做一些細緻分解。那就是說,試圖找尋一些有良好性質的子代數,並利用這些子代數和表現理論來了解整體。有點像建組合屋,先把框架(子代數)設好,再加入模組(子代數的不可約表現)組成一個複雜的結構。1990代初期,大家就發現月光頂點算子代數有一組很好的子代數,它是48個中心電荷c=½ Virasoro 代數不可約表現的張量積。這c=½ Virasoro代數的表現相對簡單,像拼積木一樣,慢慢拼湊可以得到複雜的頂點算子代數,過程類似拼圖遊戲或樂高積木,要仔細了解每個模塊的關係,小心拼湊,一不小心就要從頭開始。有趣的是拼湊的方法可以用2進位數碼來描述,不錯就是電腦和電腦溝通使用的0與1序列。宮本雅彥在2000年左右就利用這個方法,把月光頂點算子代數重新構造出來,並得到很多有關Monster的結果。這種方法可以推廣到其它的頂點算子代數,這類頂點算子代數現在稱為框架頂點算子代數。 我們的團隊對這類代數有很多的成果。首先,我們証明了如果要得到頂點算子代數,用來拼湊的2進碼必須要符合一些條件,同時,我們也得到框架頂點算子代數不可約表現的具體描述。利用這些描述,我們知道框架頂點算子代數在那種情況下是全純形,即頂點算子代數自身只有一個不可約模。我們成功的建構了很多和月光頂點算子代數相似的全純形頂點算子代數,更得到中心電荷c=24全純形框架頂點算子代數的分類。過程中,又發現了很多和Monster相關的代數,包括所謂的W代數和parafermion代數。有趣的是這些代數因其它原因,在物理學和表現理論中被廣泛研究,那為什麼它們跟Monster相關?
目前仍未有實質的答案。這些結果引領我們去處理一般中心電荷c=24全純形頂點算子代數的分類問題。經過這幾年的努力,我們已經大致了解及完成分類,但最重要的問題,即月光頂點算子代數的唯一性仍然未解決,希望對其它c=24全純形頂點算子代數的了解能幫助我們解決這個問題。
由研究生時代開始,從事怪物群和月光頂點算子代數的研究剛好30年,怪物群已經沒有最初的可怕,但它仍然是怪物,無法完全掌握它。希望有一天可以把它馴化成一隻PokéMon,嬌小可愛。
