化學是一門研究物質性質與變化的自然科學,主要探討由原子、分子和離子所組成的化合物以及它們在反應過程中所經歷的變化。早期的化學研究具有神祕色彩,例如:燃素說以及煉金術,直到十八世紀後期,拉瓦節將化學研究定量化,以氧化還原反應解釋燃燒現象,為基礎化學原理帶來了第一次革命。在這之後,道爾頓提出了劃時代的原子說,再加上許多化學家的實驗驗證下,門得列夫得以建立了元素周期表,經典化學領域的基礎才趨於完備。
將統計熱力學與量子力學引入化學領域,可視作基礎化學原理的第二次革命。在十九世紀後期,以經典熱力學為基礎,吉布斯(Josiah Willard Gibbs)所提出的吉布斯能(Gibbs free energy)與化學勢(Chemical Potential)闡明了化學平衡與相平衡等現象的本質。另一方面,奧斯特瓦爾德(Friedrich Wilhelm Ostwald)、凡特荷夫(Jacobus Henricus van’t Hoff)以及阿瑞尼斯(Svante August Arrhenius)將化學平衡與動力學的概念應用在不同化學領域,建立起化學反應的基礎物理圖像,例如像是活化能與反應速率的關係。在二十世紀初期,隨著量子力學誕生,鮑林(Linus Pauling)將量子力學引入化學,提出了電負度與混成軌域等新概念,清楚地闡述了化學鍵的本質。此後,由於計算機性能的大幅躍進,量子力學被證明可用來定量地描述複雜分子的性質,促進了量子化學等領域的興起。時至今日,科學家已經可以運用量子化學程式來計算各式各樣化學物質的幾何結構、光譜、位能面以及化學反應速率,再結合統計熱力學,進而得到物質宏觀的物理與化學性質。換言之,化學原理已經完全可以被統計熱力學與量子力學所描述,這也暗示著化學原理的基礎研究似乎已經走到了盡頭,而剩下的可能只剩化學原理的應用,然而事實真的如此嗎?
現代化學的原理建立在非相對論性量子力學,主要是在靜電假設下(與電荷的動力學無關)以庫倫作用力去敘述電荷之間的交互作用,並且將電磁場視作古典場來處理。在量子力學的框架下,真空電磁場漲落以及光與物質的強耦合效應無法被合適地敘述。量子電動力學是研究電磁作用的量子場論(電荷在量子化電磁場的動力學),也是描述光與物質交互作用最基本的理論。量子電動力學被費曼譽為「物理學的瑰寶」以及「化學背後的原理」,但在現代化學卻幾乎見不到量子電動力學的蹤跡。在絕大部分的化學系統中,靜電假設與古典電磁場是非常好的近似,科學家不需要使用量子電動力學去研究物質性質與變化。然而,在過去兩三年以來,在不外加電磁場之下(無外加光源),法國物理化學家埃貝森(Thomas Ebbesen)的團隊展示出一系列利用真空電磁場控制化學反應速率與產物的研究[1][2],打破了現代化學近一個世紀以來的認知。這個新興的領域被稱作「電磁極化子化學(polariton chemistry)」[3]或「量子電動力學化學(QED chemistry)」[4]。
電磁極化子(polariton)是由光子與電偶極激發所形成的一種準粒子(quasiparticle)。順帶一提,電磁極化子也可以由磁偶極或多極激發所形成,但非本文所關注的主題。為了幫助讀者建立電磁極化子的物理圖像,我們將氫分子與電磁極化子作為類比(請見圖一),在左圖中,兩個氫原子的1s軌域彼此交互作用,形成所謂的鍵結軌域(bonding orbital)與反鍵結軌域(antibonding orbital);在右圖中,激發態分子|e,0>(在這裡,e表示分子激發態,0表示電磁場的基態,電磁場的基態又稱為量子真空態)與光子|g,1>(在這裡,g表示分子基態,1表示電磁場的第一激發態,對應系統具有一個光子的狀態)彼此交互作用,形成所謂的「下電磁極化子(lower polariton)」與「上電磁極化子(upper polariton)」,而|e,0>和|g,1>兩個狀態之間的耦合,又稱之為量子真空漲落(quantum vacuum fluctuation)。這個物理圖像非常具有啟發性,化學的起源可視作兩個氫原子交互作用形成氫分子,而分子的形成開啟了多采多姿的化學世界。如果光與分子可以形成混成態(hybrid state),那它的物理與化學性質是什麼?這是一個多麼令人興奮的科學問題!
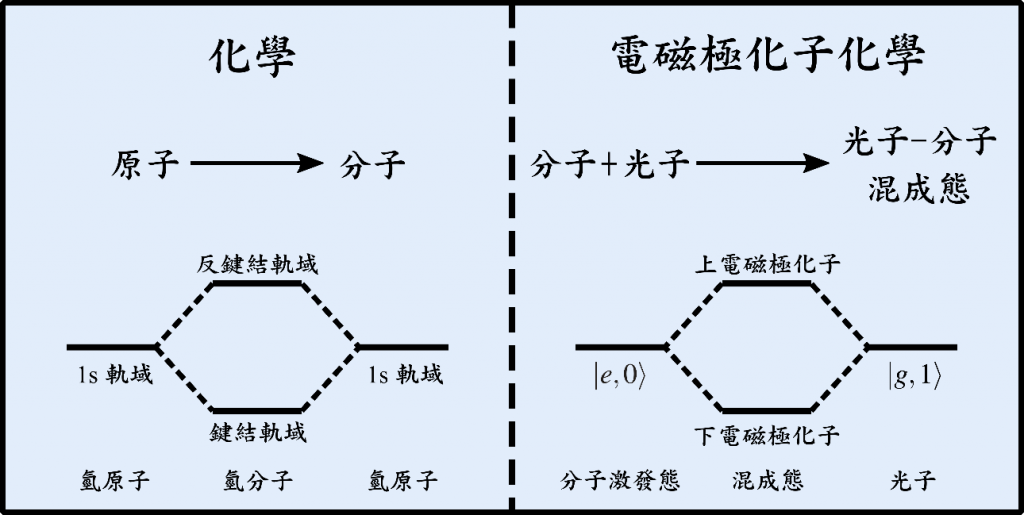
圖一:電磁極化子化學與化學的類比。分子激發態與光子所形的混成態可以用化學鍵的鍵結、反鍵結軌域理解。
事實上,電磁極化子並不是一個全新的概念。電磁極化子的理論發展可追溯1950年代,由俄國物理學家托比戈(Kirill Tolpygo)與中國物理學家黃昆(Kun Huang)分別建立模型,進而得出離子晶體中,聲子與電磁波的耦合及其色散的關聯。而電磁極化子的名稱則是在1958年由美國物理學家霍普菲爾德(John Joseph Hopfield)的論文所提出。雖然電磁極化子在固態物理領域被研究已久,但是沒有人認為電磁極化子可以影響化學反應,其主要原因包含下列兩點:第一,在一般環境下,光與分子的耦合強度遠小於分子內部的耗散,換言之,光與分子混成態非常難以形成。第二,化學反應所需要的時間遠比光與分子混成態的生命週期(lifetime)來得長,換言之,化學反應還來不及發生,光與分子混成態就消失了。
從上述兩點可以得知,要創造出光與分子混成態進行化學反應非常困難,那法國物理化學家埃貝森是怎麼做到的呢?關鍵是要創造出光與分子強耦合的條件。首先,埃貝森利用微空腔(microcavity),在微空腔內創造出電磁駐波的真空態,換言之,在特定頻率下,光子具有很高的態密度(density of states),形成光學模(photonic mode)。其次,埃貝森調整微空腔的駐波頻率,使其光學模與分子的振動模(vibrational mode)共振,在這個情形下,光學模就如同串燒的竹籤一樣,將不同分子的振動模串聯起來。根據腔量子電動力學(cavity quantum electrodynamics),如果有N個分子的振動模一起耦合,其耦合強度會變成√N倍。利用高的光子態密度以及大量分子振動模耦合,可以創造出不同分子與光之間強耦合,埃貝森稱之「振動強耦合(vibrational strong coupling)」,進而創造出光與分子混成態。根據以上的原則,埃貝森利用振動強耦合控制了裂解Si-C或Si-O鍵的反應速率,改變了化學反應的主要產物[1];除此之外,埃貝森也利用反應分子振動模、溶劑分子振動模以及光學振動模三者的耦合,大幅提升化學反應速率[2],這意味著量子真空漲落可以用來當作化學反應的催化劑!
根據埃貝森所提出的原則,電磁極化子化學最主要的問題已經被解決,人類應該可以利用量子電動力學控制化學反應。然而事實並非如此,埃貝森發現:即使調整空腔的電磁駐波頻率,使其與特定分子振動模共振,也只有一部分的化學反應會在微空腔內有所不同。這意味著,量子電動力學如何影響化學反應背後的原理機制尚未明朗,為了闡明其機制,建立全新的化學理論是必須的。埃貝森的研究引起許多理論學家的注意,然而絕大部分的理論學家都使用腔量子電動力學去描述電磁極化子化學內的現象。腔量子電動力學具有兩個自由參數:耦合強度與光學耗散(optical loss),而這兩個參數與化學分子所處於的介電環境有關。換言之,如果無法把介電環境的影響引入化學理論,我們無法預測光與分子混成態是否會形成。
為了包含介電環境對分子的影響,作者團隊將宏觀量子電動力學(macroscopic quantum electrodynamics)[5]引入化學理論。宏觀量子電動力學可視作一種有效場論或粗粒化模型(coarse-grained model),將介質環境的性質以宏觀介電函數的方式引入馬克士威方程式,再利用量子化的方法得到有效光子。除此之外,宏觀介電函數已經被用來解釋許多奈米結構的光電性質,具有相當程度的可靠性。
然而,電磁極化子參與化學反應的過程相當複雜,為了確定建立的理論具有可靠性,作者團隊決定先驗證宏觀量子電動力學是否可以用來預測分子在強耦合之下的物理性質。在過去三年以來,作者團隊基於宏觀量子電動力學,建立了適用範圍更廣的分子螢光理論[6][7]以及其分子發射功率譜理論[8]。廣義的分子螢光理論可以適用於:在複雜介電環境下,分子螢光與量子真空漲落所耦合的量子動力學,以及統一描述光與物質從弱耦合到強耦合的螢光現象,包含弗蘭克-康登(Franck-Condon)機制到電磁極化子機制(請見圖二)。換言之,作者的理論包含查恩斯(Ronald R. Chance)與西爾貝(Robert J. Silbey)在分子螢光領域的著名理論[9],兩者的理論基於古典電動力學,無法描述光與分子的強耦合。圖二為作者理論所得到的分子發射功率譜,隨著光與分子耦合強度增強,發射功率譜從弗蘭克-康登的譜線逐漸變成電磁極化子的譜線。除此之外,作者的理論可以在無自由參數下估計激子-電磁極化子的耦合強度,該理論所估計的耦合強度與卡文迪許實驗室(Cavendish Laboratory)報導的實驗結果相吻合[10]。作者的工作也被化學物理的權威期刊J. Chem. Phys.選為Editor’ Pick和Editors’ Choice in 2019。
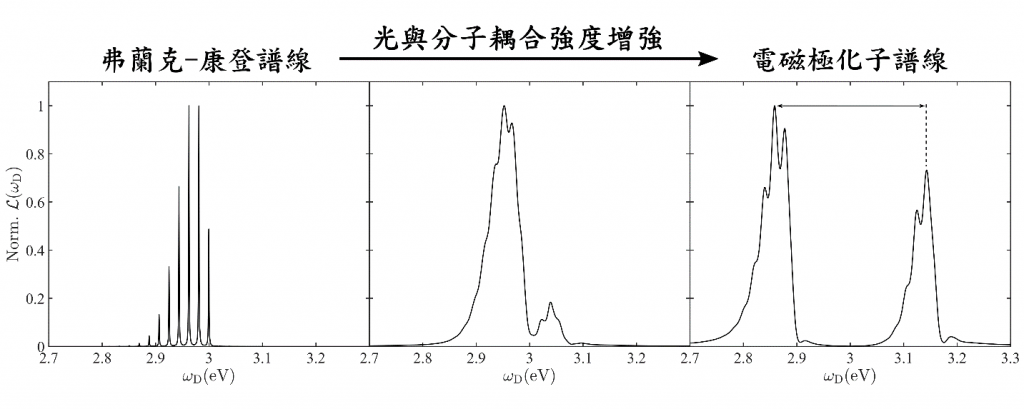
圖二: 分子的發射功率譜。隨著分子與光子耦合增強,分子的發射功率譜從弗蘭克-康登譜線(分子振動態的特徵)逐漸變化至電磁極化子的譜線。圖片從文獻[8]剪裁而來。Copyright 2019 American Institute of Physics.
致謝
作者感謝李明緯先生製作示意圖,以及李明緯先生和蔡宏昇同學校對文字。
延伸閱讀
[1] Thomas, A.; Lethuillier-Karl, L.; Nagarajan, K.; Vergauwe, R. W. A.; George, J.; Chervy T.; Shalabney, A.; Devaux, E.; Genet, C.; Moran, J.; et al. Science 2019, 363, 615−619.
[2] Lather, J.; Bhatt, P.; Thomas, A.; Ebbesen, T. W.; George, J. Angew. Chem. Int. Ed. 2019, 58, 10635−10638.
[3] Ribeiro, R. F.; Martínez-Martínez, L. A.; Du, M.; Campos-Gonzalez-Angulo, J.; Yuen-Zhou, J. Chem. Sci. 2018, 9, 6325–6339.
[4] Flick, J.; Ruggenthaler, M.; Appel, H.; Rubio, A. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 3026–3034.
[5] Vogel, W.; Welsch, D.-G. Quantum Optics; WILEY-VCH, 2006.
[6] Wang, S.; Scholes., G. D.; Hsu, L.-Y. J. Chem. Phys. 2019, 151, 014105.
[7] Wang, S.; Scholes., G. D.; Hsu, L.-Y. J. Phys. Chem. Lett. 2020, 11, 5948-5955.
[8] Wang, S.; Lee, M.-W.; Chuang, Y.-T.; Scholes., G. D.; Hsu, L.-Y. J. Chem. Phys. 2020, 153, 184102.
[9] Chance, R. R.; Prock, A.; Silbey, R. Adv. Chem. Phys. 1978, 37, 1–65.
[10] Chikkaraddy, R.; de Nijs, B.; Benz, F.; Barrow, S. J.; Scherman, O. A.; Rosta, E.; Demetriadou, A.; Fox, P.; Hess, O.; Baumberg, J. J. Nature 2016, 535, 127−130.
