「萬法皆空,因果不空」,佛學上此空非彼空;又說,因果通於三世,過去世、今世、未來世。亞里士多德在著作「形上學」探討事物的因(cause),並提出「四因論」:質料因(material cause)、形式因(formal cause)、動力因(efficient cause)、目的因(final cause)。千百年來宗教或哲學探索的因果論反映了人類對因果的好奇,是一種天性也是本能。
許多生活上遭遇的問題,我們都想知道是否存在因果關係。例如:一個患有末期癌症的路人過馬路時遭機車衝撞,除了驚嚇和皮肉傷,當下並未發現出血或器官損害等更大的問題,然而這個癌末路人在一個月後過世了,試問被機車撞到(我們表示為X)是否導致了他的死亡(表示為Y)?這樣的問題,至少牽涉哲學、醫學和法律。哲學上,X是否導致Y當然是個大哉問,除了亞里士多德,近代哲人休姆(David Hume)、彌爾(John Stuart Mill)等也都提出了因果哲學。醫學上,值得探究的是死亡也許是源自他本身的末期癌症,但是機車撞擊是否產生了肉眼不可見分子層次的傷害進而加速了死亡;法律上,直接會面對的問題是,如果行人的家屬提告機車騎士傷害甚至殺人是否成立。哲學、醫學或法律觀點的因果論各有其理論基礎及應用,本文著眼的是能否以數學定義因果。
以數學的語言來定義因果目前為止最廣為使用的應該是由美國統計學家Donald Rubin於1978年提出的反事實結果(counterfactual outcome)或潛在結果(potential outcome)架構。而反事實狀態的觀念最早甚至可回溯至十八世紀的蘇格蘭哲學家休姆(1748);在統計文獻中,廿世紀初波蘭數學家Jerzy Neyman(1923)首次在隨機農業試驗中提及。美國統計學家James Robins在1986年延伸至多重隨時間變化的因子;在資訊科學領域以圖像理論為主的因果推論(Spirites, Glymour and Scheines 1993; Pearl 1995),與潛在結果架構之理論基礎亦有共通之處。
要回答上述問題是否存在困果關係,目前擁有的資訊是不足以判斷的,亦即我們目前觀察到的資訊是:車禍發生,X=1(0為不發生),之後病人死亡,Y=1(0為未死亡),我們將病人死亡的這個變因補充為Y(X=1)或Y(1),代表的是在車禍發生情境下的死亡與否,我們觀察到的是Y(1)=1。要論證困果關係,我們需要額外的資料:如果車禍不發生X=0,那麼病人一個月後是否死亡,也就是Y(X=0)或Y(0)為何。如果Y(0)=1,也就是病人未遭遇車禍(假設除了車禍外其它條件一樣)一個月後病人還是死亡,那麼很明顯的,車禍與病人的死亡並無因果關係;但如果Y(0)=0,也就是病人若未發生車禍(其它條件一樣)的話,一個月後並不會死亡,那麼,車禍的確導致病人死亡。
上述的反事實論證提供明確且直觀的因果推論,也就是Y(X=1)≠Y(X=0)代表X和Y有因果關係,但是實務上我們幾乎無法取得完整的反事實資料。以車禍的例子而言,人死不能復生,我們無法讓病人再次復活、回到一個月前並塑造一個未發生車禍的另一段人生,來觀察一個月後他是否死亡。也就是說,對於每個人我們都只能觀察到一半的資訊,曾發生車禍的人,我們只觀察得到Y(X=1),未發生車禍的人,我們只觀察到Y(X=0)。除非物理學能突破帶來時光旅行的技術,否則因果推論僅能流於紙上談兵。不幸的是,如上述例子的單一個體因果效應(individual causal effect),在沒有很強的假設之下是無法辨識(non-identifiable)的。
相對於個體因果效應,統計學家著眼的是群體的因果效應(population causal effect),舉例而言,暴露於空氣污染,20年後台灣某區的肺癌發生率為2%,我們想知道空氣污染是否造成肺癌;另外的例子如臨床試驗,癌症病人接受藥物A的治療,5年存活率為70%,A藥物是否增加病人的存活率。這兩個例子裡,X分別是空氣污染與否、及接受藥物A與否,而Y則為發生肺癌與否(0:未發生,1:發生)、及存活與否(0:存活,1:死亡)。不過,與之前車禍例子不同的是,這裡的結果並不是單一個體的結果,而是一整個群體的平均,因此我們使用機率上的期望值(E[⋅])來描述群體平均,所以在空污的例子,我們得到的資訊是E[Y(X=1)]=0.02;在臨床試驗的例子中,E[Y(X=1)]=0.3。要進行因果推論,我們還需要收集的資訊是E[Y(X=0)],亦即沒有暴露於空污的肺癌發生率、及未接受藥物A的存活率,E[Y(X=1)]≠E[Y(X=0)]代表群體因果效應的存在。
群體因果效應的可辨識性(identifiability)仰頼一些假設。首先,Y(X=x), x=0 or 1,我們簡寫為Y(x),它雖代表的是肺癌的發生與否,但它其實是一個虛擬的情境:Y(x)代表的是空污暴露為x的情境下,肺癌發生與否。若我們以整個台灣人口為研究對象,而把台灣人口想像成圖一右邊的菱形,那麼我們的因果推論實驗應該將全台灣人口暴露在空污(圖一右上面的藍色菱形),觀察20年後肺癌發生個數(藍色菱形中的藍色圓點)並計算發生率E[Y(1)],接下來用時光旅行回到20年前實驗開始的時候,這次讓全台灣人口暴露在非空污的環境(圖一右下面的橘色菱形),觀察20年後肺癌發生個數(橘色菱形中的橘色圓點)及發生率E[Y(0)],若E[Y(1)]≠E[Y(0)]則空污導致台灣人口肺癌。
上述的實驗設計同樣地需要時光旅行的科技,雖然有助於我們直觀地定義何謂因果效應,但實務上不可行。我們實際上得到的資料是(X,Y)(即圖一左邊的藍色鑽石形及橘色三角形),而非(Y(1),Y(0))(即圖一右邊的藍色及橘色菱形)。我們做一個大膽的假設:左邊藍色鑽石形的資料可以外推補齊缺漏的三角形,而變成右邊完整的藍色菱形,相同地,左邊橘色三角形的資料亦可以外推補齊缺漏的鑽石形,而變成右邊的橘色菱形,這個假設以數學語言描述為:Y(x)⊥X,鑽石型族群(或三角形族群)的反事實結果與實際上暴露空污與否獨立。稍後我們解釋這個假設的涵義,但在這個假設之下,左邊的實際資料給予我們相當於需要時光旅行技術才能得到的資訊。因此,我們在實際資料下進行簡單條件期望值的計算即等同於反事實結果的期望值:E[Y|X=x]=E[Y(x)],也就是說,我們只需要在有空污的地區(E[Y|X=1])和非空污的地區(E[Y|X=0])進行肺癌發生率的計算,就能分別代表全台灣接受空污暴露(E[Y(1)])及未受空污暴露下(E[Y(0)])肺癌的發生率。這個大膽的假設,稱之為可互換性(exchangeability),這個假設的強大之處在於,它帶來了跟時光旅行一樣的效果。
我們用臨床試驗的例子來談一下可互換性假設的內涵。我們同樣使用圖一左邊代表臨床試驗的的實際資料,藍色鑽石形代表接受藥物A的病人,藍色圓點代表死亡的病人,橘色三角形代表未接受藥物A的病人而橘色圓點為死亡的病人。此外,我們假設病人接受藥物A與否是隨機的,亦即此研究為隨機臨床試驗(randomized clinical trial)。因為隨機的關係,鑽石形族群與三角形族群應該在各個方面都很類似,包括性別比例、年齡分布、教育程度、基因形態等;若此兩族群的樣本數很大(例如超過一萬人),那麼我們甚至可能認為這兩個族群幾乎是一樣的。所謂一樣,可以想像成,每個藍色族群的病人,都可以在橘色族群病人中找到跟他/她各方面都很類似的人,除了接受藥物與否。因此,藉由隨機分配我們模擬出了一個時光旅行的效果,本來應該藉由時光旅行才能產生的圖一右,因為隨機分配X的實驗設計,兩個本應屬於平行時空的藍色與橘色族群,同時存在於我們的試驗中。隨機分配之下,導致鑽石形和三角形族群的高度相似性,亦可詮釋為這兩個族群是可互換的。因為他們可互換,我們才會說他們的潛在結果Y(x)與實際上他們接受治療與否X是獨立的,Y(x)⊥X;因為可互換,如果反過來讓鑽石形族群不接受治療(改為橘色),而讓三角形族群接受治療(改為藍色),得到的實驗結果將一樣;也因為可互換,我們才能外推鑽石形去補足缺漏的三角形造就完整的菱形,所以,左邊實際資料的條件機率估計會等價於右邊時光旅行設計下的實驗結果。
讓我們再回空污研究的例子,可互換性假設在這個例子為:暴露在空污下的台灣族群和非空污下的台灣族群可互換。但是,空污的暴露X並非如臨床試驗例子的X是隨機分配的,可互換性的假設在這個例子可能並不成立,例如,比起高空污的西半部,處於低空污的花東地區較多原住民人口,因此基因型態就會有顯著的不同。若忽略了此一差異,那麼單純比較高空污和低空污的肺癌發生率,我們無法區分究竟發生肺癌的差異是來自空污還是來自基因,此一現象我們稱之為干擾(confounding)。當相關性受到干擾時,它就無法代表因果性;反之,當相關性沒有其它干擾時,就等同於有可互換性,因此實際資料下觀察到的相關性就有因果性的詮釋。那麼,在空污的例子中是否完全無法研究其因果性呢?其實未必,如果我們知道原住民族群的比例是個干擾因子,那麼我們可以用統計方法去校正此一干擾因子,例如,我們簡單將相關性的比較侷限於非原住民族群。或更複雜一些,若有多重的干擾因子Z,例如教育程度、職業、年齡等,也會干擾空污和肺癌的相關性,那麼我們可以使用更複雜的統計模型去校正這些因子,以期達到條件可互換性(conditional exchangeability):Y(x)⊥X|Z。所謂的條件可互換性,就是雖然就整體而言沒有互換性,但若能把研究族群的原住民比例、教育程度、職業、年齡都控制為一樣,那麼在這個小小的次族群中,可互換性則可成立。那麼在這個假設之下,統計方法提供的相關性估計也可以詮釋為因果性。
思考因果性,使用反事實結果或時光旅行的想法是一種很好的邏輯訓練,雖然時光旅行在實務上還不可行,但這種思考訓練能讓我們抽離現實,以較形而上的方式定義因果。接下來,可以用隨機試驗的方式來想像如何落實為一個可操控的研究,當然它有時可行(如:臨床試驗)、有時礙於倫理和資源亦仍不可行(如:空污研究)。最後,常常我們只能藉由觀察型研究,以相關性替代因果性,此替代成立需仰頼條件可互換性,並藉由統計方法充分校正達成此一互換性的干擾因子。
筆者認為人類對於因果性的好奇是本能,以數學語言來描述因果是一個重要的開始,它讓形而上層次的因果哲學,藉由數學符號回到我們身處的物理世界;它也讓因果的直觀性落實到可溝通運算的客觀符碼,搭配數理統計理論可以進一步挑戰非直觀、幽微且複雜的因果問題。
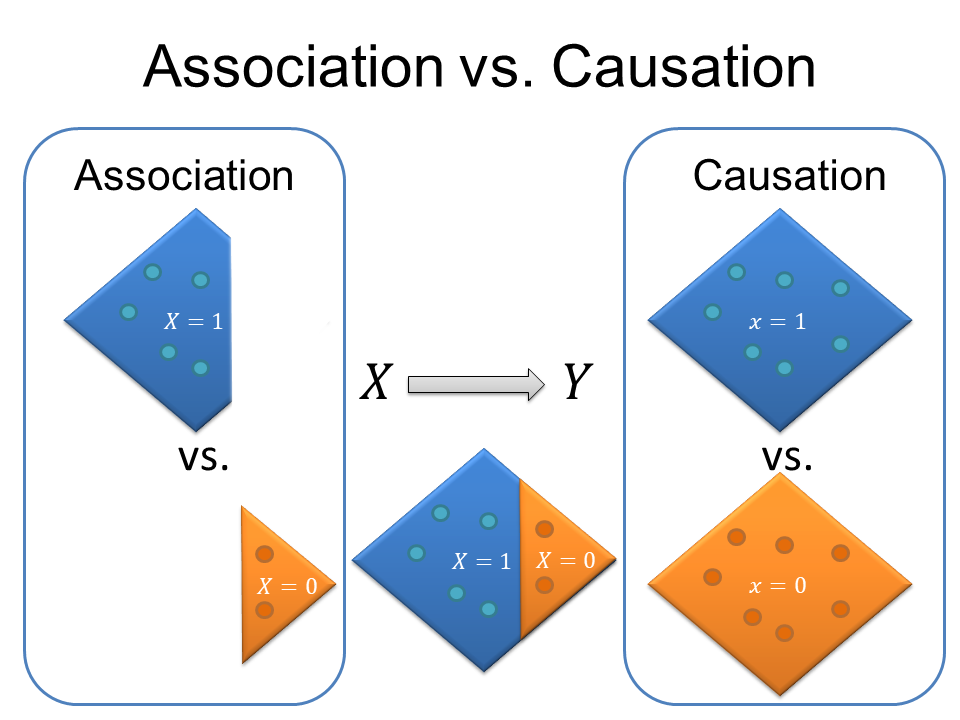
圖一,因果性(causation)和相關性(association)的區別。圖形中圓形小點代表Y=1的發生。(下圖重製改編Hernan and Robins之圖1.1)
參考文獻
Hume, D. (1748). An Enquiry Concerning Human Understanding. Reprinted, 1958, LaSalle, IL: Open Court Press.
Neyman, J. (1923). Sur les applications de la thar des probabilities aux experiences Agaricales: Essay des principle. Excerpts reprinted (1990) in English (D. Dabrowska and T. Speed, translators) in Statistical Science 5, 463-472.
Rubin, D. (1974). Estimating causal effects of treatments in randomized and non-randomized studies. Journal of Educational Psychology 66, 688-701.
Robins, J. (1986). A new approach to causal inference in mortality studies with sustained exposure period – application to control of the healthy worker survivor effect. Mathematical Modelling 7, 1393-1512.
Spirites, P., Glymour, C. and Scheines, R. (1993). Causation, Prediction, and Search. Cambridge, MA: MIT Press.
Pearl, J. (1995). Causal diagrams for empirical research (with discussion). Biometrika 82, 669-710.
Hernan, M. A. and Robins, J. M. Causal Inference (unpublished book draft)
VanderWeele, T. J. (2015). Explanation in Causal Inference: methods for mediation and interaction. Oxford University Press.
