面臨不確定因素時，人們做決策的行為模式，一直是許多領域的重要研究課題。其中探索的焦點之一，是設法找出並且解釋人們在受到不確定性的影響之下，所表現在認知上的偏誤。

有別於一般利用特定的實驗、或問卷方式，本文藉由分析一組樂透彩券投注者的選號資料，了解在現實生活有大量參與者的遊戲裡，人們詮釋由於機率所導致的不確定性，而產生的偏誤，並更進一步建構其行為的動態模式。

藉著一個低成本的機會，實現迅速成為千萬甚至億萬富翁的願望，樂透遊戲能得到大眾的接受與喜好，自是上不難理解。文獻中以經濟理論或定性方式，解釋為什麼規避風險的理性消費者，願意參與不公平的遊戲，已有廣泛的探討，對投注市場的定量分析，以及相應的模型建構的研究，卻顯得不足。

我國公益彩券依據1995年7月公布施行的《公益彩券發行條例》，自1999年12月1日開始發行。第一代可以自行選號的樂透彩券，首先由台北富邦銀行於2002年取得授權營運。投注方式為50元一注，從1到42選6個號碼，自行選號與電腦選號並行，每週搖號開獎兩次。我們分析的資料，是2002與2003兩年，連續共203期樂透彩劵，自選號碼組合的全部紀錄(期間自選號碼彩票售出1,679,676,226張，佔總銷售的61%)。

一、三個因素

資料分析的結果，顯示樂透投注者選取號碼，受到三個因素影響：上一期開獎的中獎號碼，號碼過去的中獎頻率，以及上一期樂透投注者選擇的號碼[1]。 以下分別簡述，這三個因素如何影響投注者的選號行為。

（一）賭徒的謬誤 (the gambler’s fallacy)

在純粹是由機率決定輸贏的賭博遊戲裡，經常可以看到，參與的賭徒有種傾向，相信當期的結 果，不會在下一期重複出現。類似的錯誤詮釋機率法則的現象，文獻中稱之為賭徒的謬誤。 Tversky 與 Kahneman (2002年諾貝爾經濟學獎得主)將其擴充，提出「小數法則」(the law of small numbers)現象[2]，並進一步，將此現象歸因於代表性簡捷推論法 (representativeness heuristic)所造成的認知偏誤[3]。

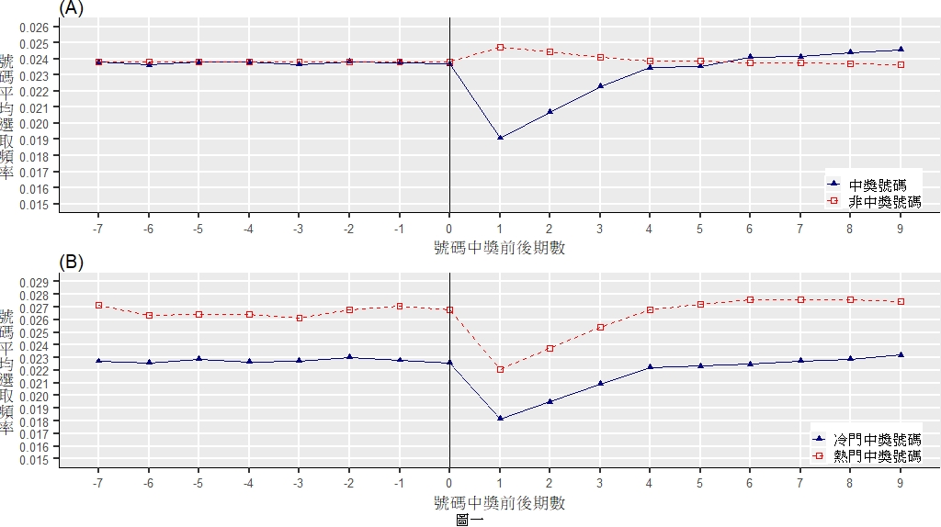
以我們分析的樂透資料為例，圖一(A)的藍色折線，每個水平座標為 x 的實心三角形，其垂直座標表示第 t 次遊戲的6 個中獎號碼，在第 t+x 次遊戲，被選取的平均頻率(對 6 個中獎號碼，以及資料範圍內的各個 t 次遊戲做平均)。 同樣在紅色點線上，每個水平座標為 x 的正方形，其垂直座標表示，第 t 次遊戲的36個非中獎號碼，在第 t+x 次遊戲，被選取的平均頻率 (對 36 個非中獎號碼以及資料範圍內各個 t 次遊戲做平均)。 投注者若是隨機選號，每個號碼被選中的頻率，應該近似1/42=0.0238。 圖一(A)顯示，中獎號碼在下一期被選取的頻率，明顯的從接近0.0238下降到0.019 ，減少 0.0046 (p<0.001)，非中獎號碼的平均被選取頻率，維持在0.0238附近，只有微幅波動，兩相對照，清楚表示賭徒謬誤現象的存在。

（二）機器有問題

受到賭徒謬誤的影響的同時，樂透參與者也展現一個對立的行為模式，特別青睞於過去中獎頻率較高的號碼。他們認為這些號碼中獎率高，並非偶然，很可能是開獎機器的本身問題所造成。圖一(B)即描述此一有趣的現象。首先，我們將當期中獎號碼分成兩類，在過去99期(包含當期)不少於7次中獎次數，列為熱門中獎號組，其餘則歸為冷門中獎號組。然後計算這兩組號碼，在當期前後數期，被投注者選中的平均頻率。圖中的橫軸座標與縱座標，和圖一(A ) 相同，亦即每個水平座標為 x 的正方形或實心三角形，其垂直座標值表示，第 t 次遊戲的熱門中獎號組或冷門中獎號組，在第 t+x 次遊戲，被選取的平均頻率(分別對熱門與冷門中獎號碼組，以及資料範圍內各個 t 次遊戲做平均)。

圖一(B)顯示兩個特性，第一，熱門中獎號組與冷門中獎號組，都受到賭徒謬誤的制約，被投注者選中的平均頻率，在中獎號碼公佈的次一期，都顯著下降。前者(紅色正方形點線)從0.0268降至0.0221，下跌17.54%（p < 0.0001），後者(實心三角形藍色折線)從0.0226降至0.0011，下降19.91%（p < 0.0001）。第二個特性，熱門中獎號組的平均被選中頻率，在不同的前後期，一致性的顯著高於冷門中獎號組的平均被選中頻率，而後者的頻率變化趨勢，與隨機選號頻率的走勢(圖一(A)的藍色折線)，幾無二致。投注者偏好熱門中獎號碼的行為，表露無遺。

（三）選號如同覓食

圖一(A)與(B) 均顯示，中獎號碼的平均選中頻率，雖然受到賭徒謬誤的影響而下跌，但之後，逐漸爬升，恢復至隨機選取頻率的平均水準。我們觀察到，中獎號碼的平均選中頻率，即使沒有賭徒的謬誤，亦呈現出另一方向回歸平均，由上向下的現象。在圖二(A) 中，紅色正方形的時間數列，代表當期非熱門中獎號碼組中(如圖一(B)所定義)，前三個選取頻率最高，但卻未中獎的的號碼的平均選取頻率，藍色實心圓的數列，則代表同樣三個號碼，在下一期被選取的頻率，資料有203期，所以序列總共有104個時間點，與圖二(A)反面對稱，圖二(B)中的藍色實心圓的時間數列，代表當期冷門中獎號碼組中(如圖一(B)所定義)，三個選取頻率最低，而且沒有中獎的號碼的平均選取頻率，而紅色正方形的數列，則代表同樣三個號碼，在下一期被選取的頻率資料。

圖二(A)及(B)的藍色實心圓與紅色正方形的兩組數列，平均值明顯有高低之分，對其分別進行配對 t 檢驗，兩組數列平均值差距，分別為 -0.0019 （= 0.0292 – 0.0311 ) 和 0.0025 （= 0.0183 – 0.0158）。均有顯著差異（p < 0.001)）。圖二(A)與(B)顯示，投注者選號的行為類似覓食，會去曾經發現有食物的地方試試，一旦希望落空，則易地他求(如圖二(A))，目標則是曾經發現有食物，且之前較少去的地方(如圖二(B))。

二、延伸與結語

利用前述三項因素：賭徒的謬誤，熱門中獎號碼的偏好，以及選取號碼回歸平均，我們引進下面時間序列模型：

Q(i,t) = α + β_1Q(i,t-1) + β_2HIT(i,t-1) + β_3HOT(i,t-1) + ε(t)，(1)

以闡述投注者選號行為的動態結構。 模型(1)中，變數Q(i,t) 是樂透玩家在第 t 期時選取號碼 i 的平均頻率；如果號碼 i 在第 t-1期為中獎號碼，HIT(i,t-1) 的值為 -1，否則為 0；如果號碼 i 在第 t-1 期，為之前圖一(B)所定義的熱門中獎號，HOT(i,t-1) 的值 為 +1, 否則為 0 。 統計分析的結果 β_1， β_2與 β_3，均顯著為正 (p < 0.001) ，解釋力達到 0.6670。變數值為正的β_1，反應第三項因素所描繪，投注者選號行為有回歸平均值的現象 ， β_2與 β_3顯著為正，則分別證實，投注者受到第一與第二項因素影響，而產生的認知偏誤。

結合傳統的看法與新的觀點，我們介紹了一個隨機模型，就一個真實機率遊戲，刻劃其大量參與者的選擇行為，不僅更深入的了解，人們因不確定性而造成的行為偏誤，類似的時間序列模型方法，相信也可以作為分析其他機會遊戲資料的借鏡。

參考文獻

[1] Ho, H.-C, Lee, S.C., and Lin, H.W. (2019). Modeling of how lotto players select their number combinations dynamically. International Gambling Studies,19, 200-219.
[2] Tversky, A., & Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletins,
76, 105-110.
[3] Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: heuristics and biases.
Science,185, 1124-1131.